DENA: Réseaux dynamiques en expansion : modélisation, analyse et simulation de l'exploration spatiale à plusieurs échelles sous contraintes

Des sujets différents, une problématique commune

Comment les informations ou les rumeurs évoluent-elles au sein d’un réseau numérique ou social ? Comment les champignons ou les plantes envahissent -ils un milieu pour une recherche « optimale » de nutriments ? Comment les agents pathogènes se propagent-ils au sein d’une population ? Comment les marchandises, l'énergie, l'argent circulent au sein d'une économie ? Autant de sujets qui semblent à priori n’avoir aucun point commun.

Pourtant, l’évolution de tous ces phénomènes est liée à la même problématique, à savoir la dynamique des processus de diffusion à travers un réseau évolutif d’agents connectés. La description mathématique peut s'appuyer sur des modèles très similaires. Ce projet de recherche fondamentale consiste donc à analyser, modéliser et caractériser la dynamique la plus générale d’expansion d'un réseau d’agents en interaction, sous diverses contraintes, à petite et grande échelle.

Un modèle mathématique général

Le choix de l’étude expérimentale s’est porté sur un exemple archétypal : la croissance hyphale du champignon filamenteux Podospora anserina. 

Ce modèle-jouet, à la fois versatile, concret (et peu onéreux !) permet une validation in vivo des modèles mathématiques.
Pour atteindre son objectif, le projet va recourir à :

- de la modélisation, de l’analyse mathématique et des simulations numériques :
traitées à la fois à l'échelle microscopique, c'est-à-dire à l'échelle de la croissance locale des hyphes (on s’intéresse à la vitesse locale de propagation des apex ou pointes, à la distribution des angles lors des ramifications primaire – aux apex – et secondaire – le long de l’hyphe) et à l'échelle macroscopique. Décrire cette expansion à grande échelle (comme un front de propagation) à partir de la dynamique locale microscopique des hyphes d'un organisme fongique constitue un point essentiel de l’étude, permettant de relier la dynamique à grande échelle à la ramification à petite échelle.

- Des réalisations expérimentales :
celles-ci permettent d'éclairer comment les champignons filamenteux adaptent leur croissance grâce à la structuration de leur réseau mycélien, et ce, de la manière la plus efficace possible lorsque les hyphes sont perturbées ou entravées dans leur exploration environnementale du fait de contraintes externes : physico-chimiques comme la présence de diverses sources de carbone, au contraire la carence en nutriments, un gradient de température, de nutriments, de poison… ; mécaniques comme la présence d’un obstacle , biologiques comme la présence d'un autre organisme ou la suppression locale du réseau mycélien).

Le couplage de la modélisation mathématique avec ces réalisations expérimentales permet d’obtenir un modèle de référence, décrivant les processus d'interaction entre petite et grande échelle, et dont les paramètres sont facilement modifiables pour l’adapter à d’autres types de contraintes ou de conditions de croissance.

Résoudre un autre défi majeur  

A l’interface entre plusieurs disciplines, ce projet permet d’enrichir les connaissances scientifiques en biologie et physiologie des champignons filamenteux, en post-traitement des données dynamiques spécifiquement acquises, mais aussi en modélisation mathématique/statistique comme en simulation numérique de réseaux multi-échelles complexes biologiques contraints.

Sa valeur ajoutée essentielle réside dans son aspect interdisciplinaire : la collaboration effective entre mathématiciens (LJAD, INRIA et collaborations extérieures à Orsay et à l’École Polytechnique), biologistes et physiciens (collaborations extérieures à Paris 7) permettra d’aller au-delà de la compréhension de tels réseaux aussi complexes pour se tourner vers un autre défi majeur : celui de maîtriser leur dynamique, par exemple pour le contrôle de la croissance des champignons ou de plantes, la propagation de maladies, de « fake news », les réseaux sociaux…

L’Académie Systèmes Complexes soutient ce projet de recherche à travers le financement d’un workshop interdisciplinaire organisé à Nice les 22 et 23 Novembre 2017.

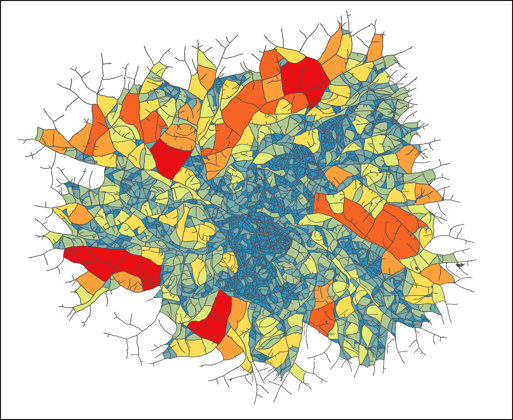
Légende photo : Cartographie d’un réseau de champignon filamenteux. Les couleurs représentent la densité du réseau : les zones les plus denses apparaissent en bleues puis vert, les zones les moins denses, en jaune, orange, rouge. L’image correspond à 20h de croissance, le champignon présenté est Podospora anserina. 
Dikec et al. 2020