Ce projet de recherche fondamentale en mathématiques s’intéresse à des problématiques relevant plus particulièrement du périmètre de la Géométrie Algébrique et de l’Algèbre Commutative. Il mobilise des mathématiciens mais aussi des informaticiens. Les résultats obtenus pourraient, à long terme, avoir également des répercussions dans le domaine du traitement des données et dans celui de la sécurité des systèmes informatiques.
Une collaboration effective entre mathématiciens et informaticiens
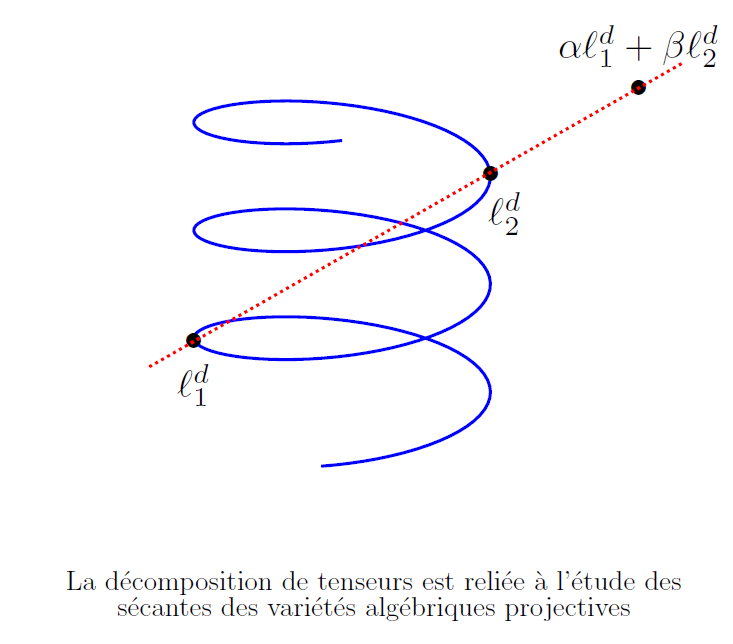
Les chercheurs de "TENPO" s‘attachent à définir la décomposition d’un tenseur* symétrique (polynôme homogène), en explorant les connexions entre l’interpolation de polynômes et la décomposition tensorielle.
Pour ce faire, ce projet fait essentiellement appel à des mathématiciens travaillant en Géométrie Algébrique et Algèbre Commutative (LJAD) qui étudient l’interpolation des polynômes puis des mathématiciens versés aussi en informatique et en contact avec d'autres informaticiens de l’équipe AROMATH de l’INRIA.
Ces derniers se penchent, quant à eux, sur la décomposition tensorielle, qui s'avère très utile pour tout ce qui a trait aux tests numériques.
Des répercussions au-delà des mathématiques
Trou 
La réalisation de ce travail en Géométrie Algébrique et en Algèbre Commutative peut aussi avoir, sur le long terme, des répercussions bien au-delà des mathématiques pures.
En effet, les résultats de ces recherches pourraient avoir un fort impact dans le domaine du traitement des données massives ainsi que dans celui de la sécurité des systèmes informatiques de toutes sortes.
Les résultats obtenus dans le cadre de ce projet seront présentés à des conférences internationales de prestige et publiés dans des journaux de haut niveau.
Ils feront aussi l’objet d’une présentation à une école CIMPA à Hanoi en Mars 2019. Enfin, une conférence internationale sur le sujet sera également organisée à Nice, offrant une large visibilité à Université Côte d’Azur (UCA) sur cette thématique.
| L’Académie Systèmes Complexes apporte son soutien à ce projet de recherche fondamentale de haut niveau en octroyant un financement de 6k€ pour couvrir le coût d’un stage et pour que la collaboration initiée entre le laboratoire des mathématique LJAD et l’équipe AROMATH d’INRIA puisse se poursuivre. |
Pour en savoir davantage sur ce projet, retrouvez le projet scientifique détaillé en cliquant ici.
* Un tenseur symétrique P est un polynôme homogène en n variables de degré d. Pour calculer sa valeur P(a) en un n-tuple donné a, il faut faire un grand nombre d’opérations élémentaires (additions et multiplications). Une décomposition de ce tenseur P est une représentation comme une somme des puissances de formes linéaires. Cela diminue fortement le nombre d'opérations élémentaires nécessaires pour calculer P(a).
Les principales avancées
- Participation et exposé à la conférence internationale Géométrie Algébrique, Cetraro 5-16 septembre 2018.
- Organisation, participation et exposé à la conférence internationale et Ecole CIMPA Arrangements d’hyperplans, Hanoï 9-23 mars 2019.
- Participation et exposé à la conférence internationale Singularités, Cargèse, 29 avril-4 mai 2019.
- Organisation, participation et exposé à la conférence internationale et Ecole Diviseurs libres, Bucarest 9-30 mai 2019. Parmi les conférenciers, Laurent Busé (INRIA).
- Organisation, participation et exposé à la conférence internationale Propriétés de Lefschetz, CIRM Luminy, 13-18 octobre 2019.
- Exposé au séminaire de Géométrie Algébrique, Humboldt University, Berlin, 20-22 novembre 2019.
- Publications de 14 articles et 2 prépublications.
- Collaboration avec Giovanna Ilardi et Armando Cerminara (Naples).
- Poursuite de la collaboration avec Laurent Busé et Bernard Mourain (INRIA, projet AROMATH).
Références : les articles de rang A publiés à partir 2019
- En savoir plus
-
1. (with G. Sticlaru) : Computing the monodromy and pole order filtration on Milnor fiber cohomology of plane curves, Journal of Symbolic Computation 91(2019), 98-115.
2. (with D. Ibadula and D. A. Măcinic) : Freeness for 13 lines arrangements is combinatorial, Discrete Mathematics 342 (2019), 2445–2453.
3. (with G. Sticlaru) : Saturation of Jacobian ideals : some applications to nearly free curves, line arrangements and rational cuspidal plane curves, J. Pure Appl. Algebra 223 (2019), no. 12, 5055–5066.
4. (with G. Sticlaru) : Line and rational curve arrangements, and Walther’s inequality, Rend. Lincei Mat. Appl. 30 (2019), 615–633.
5. On the Milnor monodromy of the irreducible complex reflection arrangements, J. Inst. Math. Jussieu 18 (2019), 1215–1231.
6. (with G. Sticlaru) : On supersolvable and nearly supersolvable line arrangements, Journal of Algebraic Combinatorics 50 (2019), 363-378.
7. On rational cuspidal plane curves and the local cohomology of Jacobian rings. Comment. Math. Helv. 94 (2019), 689–700.
8. (with G. Sticlaru) : Computing Milnor fiber monodromy for some projective hypersurfaces, In : A panorama of singularities, pp. 31–52, Contemp. Math. 742, Amer. Math. Soc., Providence, RI, 2020.
9. (with L. Busé and G. Sticlaru) : Freeness and invariants of rational plane curves, Mathematics of Computation 89 (2020), 1525–1546.
10. (with T. Abe) : On complex supersolvable line arrangements, Journal of Algebra 552 (2020), 38–51.
11. (with G. Sticlaru) : Deformations of plane curves and Jacobian syzygies, Math. Nach. 293 (2020), 475–490.
12. (with R. Gondim, G. Ilardi) : Higher order Jacobians, Hessians and Milnor algebras, Collectanea Mathematica DOI : 10.1007/s13348-019-00266-1
13. (with G. Sticlaru) : Plane curves with three syzygies, minimal Tjurina curves, and nearly cuspidal curves, Geometriae Dedicata DOI : 10.1007/s10711-019-00485-7
14. (with G. Sticlaru) : Deformations of plane curves and Jacobian syzygies, Math. Nach. 293 (2020), 475–490.

















