- Science et Société,
TENPO : Décomposition des tenseurs et interpolation polynomiale
Ce projet de recherche fondamentale en mathématiques s’intéresse à des problématiques relevant plus particulièrement du périmètre de la Géométrie Algébrique et de l’Algèbre Commutative. Il mobilise des mathématiciens mais aussi des informaticiens. Les résultats obtenus pourraient, à long terme, avoir également des répercussions dans le domaine du traitement des données et dans celui de la sécurité des systèmes informatiques.
Une collaboration effective entre mathématiciens et informaticiens
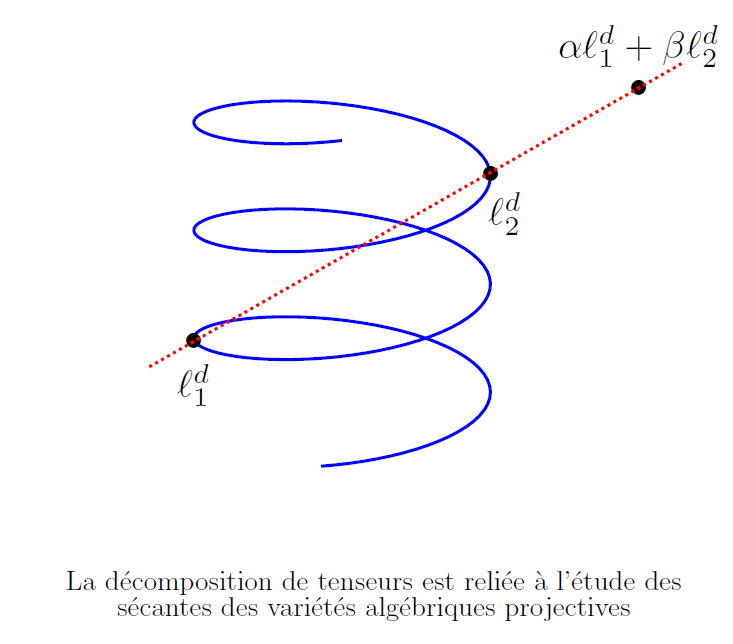
Ces chercheurs s‘attachent à définir la décomposition d’un tenseur* symétrique (polynôme homogène), en explorant les connexions entre l’interpolation de polynômes et la décomposition tensorielle.
Pour ce faire, ce projet mobilise essentiellement des mathématiciens travaillant en Géométrie Algébrique et Algèbre Commutative (LJAD) qui étudient l’interpolation des polynômes puis des mathématiciens versés aussi en informatique et en contact avec d'autres informaticiens de l’équipe AROMATH de l’INRIA.
Ces derniers se penchent, quant à eux, sur la décomposition tensorielle, qui s'avère très utile pour tout ce qui attrait aux tests numériques.
Des répercussions au-delà des mathématiques

En effet, les résultats de ces recherches pourraient avoir un fort impact dans le domaine du traitement des données de type Big Data ainsi que dans celui de la sécurité des systèmes informatiques de toute sorte.
Les résultats obtenus dans le cadre de ce projet seront présentés à des conférences internationales de prestige et publiés dans des journaux de haut niveau.
Ils feront aussi l’objet d’une présentation à une école CIMPA à Hanoi en Mars 2019. Enfin, une conférence internationale sur le sujet sera également organisée à Nice, offrant une large visibilité à Université Côte d’Azur (UCA) sur cette thématique.
| L’Académie des Systèmes Complexes soutient la recherche fondamentale de haut niveau en octroyant un financement à ce projet qui permettra notamment de couvrir le coût d’un stage et poursuivre ainsi la collaboration initiée entre le JAD et l’équipe AROMATH d’INRIA. |
Pour en savoir davantage sur ce projet, retrouvez le projet scientifique détaillé en cliquant ici.
* Un tenseur symétrique P est un polynôme homogène en n variables de degré d. Pour calculer sa valeur P(a) en un n-tuple donné a, il faut faire une grand nombre d’opérations élémentaires (additions et multiplications). Une décomposition de ce tenseur P est une présentation comme une somme des puissances de formes linéaires. Cela diminue fortement le nombre des opérations élémentaires nécessaires pour calculer P(a).

















